Utah FORGE Native State Model
Problem Statement
The Frontier Observatory for Research in Geothermal Energy (FORGE) site is a multi-year initiative funded by the U.S. Department of Energy for enhanced geothermal system research and development. This example presents the development of the native state simulation (i.e., pore pressure, stress, and temperature) of the FORGE site using material property values obtained from the site characterization activities. A detailed description can be found in Liu et al. (2022).
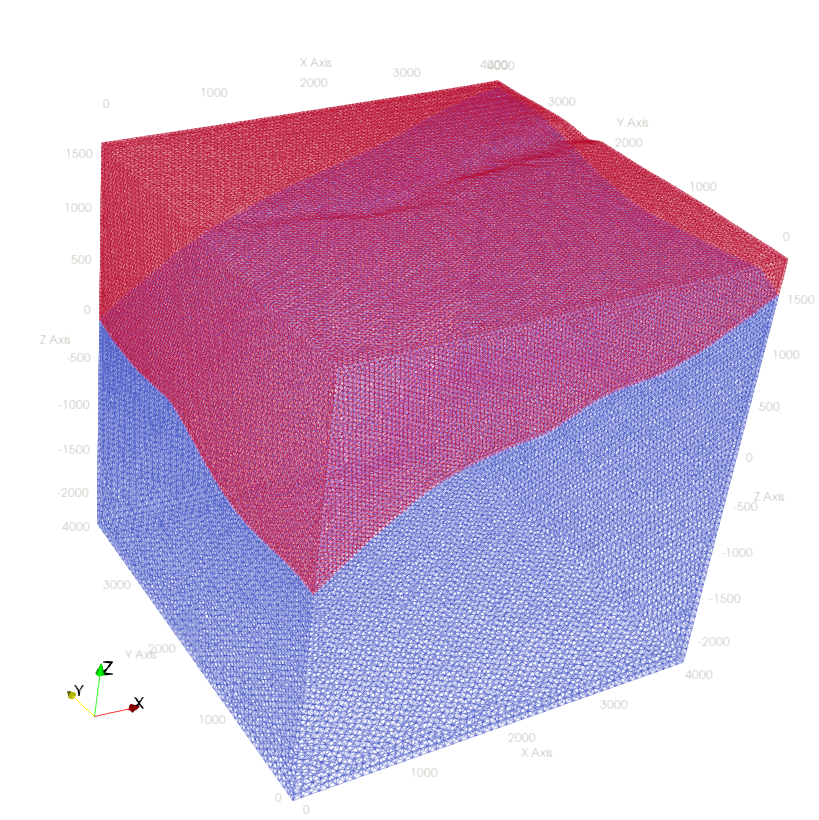
Figure 1: Geometry and finite element mesh of the FORGE site model.
The FORGE site is located inside the southeast margin of the Great Basin near the town of Milford, Utah. The site stratigraphy is divided into two units composed of crystalline plutonic rock and overlying bedded alluvium and volcanic deposits. A finite element mesh was customized to accurately capture the two units with a surface to separate them as shown in Figure 1. In FALCON input file, this mesh is imported via
[Mesh]
file = forge_model80x40x40.msh
use_displaced_mesh = false
[]
This *.msh input file can be downloaded from the GDR website.
Input File
Governing Equations
The native state model considers geomechanics, fluid flow, and heat transfer. Instead of using Actions, such as the PorousFlowUnsaturated Actions in the previous RTES examples, we now build the THM coupled governing equation using Kernals from the scratch. First, we define the primary unknows, which are the pore pressure, temperature, and displacement as
[Variables]
[./pressure]
[../]
[./temperature]
scaling = 1E-8
[../]
[./disp_i]
scaling = 1E-10
[../]
[./disp_j]
scaling = 1E-10
[../]
[./disp_k]
scaling = 1E-10
[../]
[]
Note the scaling factors are used to achieve a better convergence rate, see the instruction for details.
The complete governing equations of the THM coupled problem are detialed in the theory page. For this FORGE simulate case, we simplify them as where and denote pore presure and temperature, while and are the stress and identity tensors. is the Biot’s constant, and is the thermal expansion coefficient for rocks, represents the density of porous media including both rock skeleton and filled fluids, and the gravity vector. For the mass convervatiom equation, where is the displacement vector of the solid phase, is the permeability tensor of porous media, is the fluid flow source, and is the Biot’s modulus. For the energy conservation equation, is the thermal conductivity tensor for whole rock media, the specific enthalpy for phase j, is the advective Darcy flux, and is the heat source.
Note the objective of this simulation is to obtain the native state of the FORGE site with a steady state simulation. The pressure () and temperature () time derivative terms, in above equations are omitted. Given the extreme low permeability, the heat conduction term due to fluid flow is also omitted. We also assume the fluid in FORGE site is in the liquid state under the native state. With above reasoning, the Kernals section for the governing equation is listed in the following:
[Kernels]
[./Darcy_flow]
type = PorousFlowAdvectiveFlux
fluid_component = 0
variable = pressure
gravity = '0 0 -9.8'
[../]
[./heat_conduction]
type = PorousFlowHeatConduction
variable = temperature
[../]
[./grad_stress_i]
type = StressDivergenceTensors
variable = disp_i
component = 0
[../]
[./grad_stress_j]
type = StressDivergenceTensors
variable = disp_j
component = 1
[../]
[./grad_stress_k]
type = StressDivergenceTensors
variable = disp_k
component = 2
# displacements = 'disp_i disp_j disp_k'
[../]
[./poro_i]
type = PoroMechanicsCoupling
variable = disp_i
porepressure = pressure
component = 0
[../]
[./poro_j]
type = PoroMechanicsCoupling
variable = disp_j
porepressure = pressure
component = 1
[../]
[./poro_k]
type = PoroMechanicsCoupling
variable = disp_k
porepressure = pressure
component = 2
[../]
[./weight]
type = Gravity
variable = disp_k
value = -9.8
[../]
[]
In order to obtain the secondary variables, such as the stress tensor, fluid density, viscosity, etc, the AuxKernels section needs to explicitly request these output.
Initial and boundary conditions
For fluid flow field, as shown in Figure 2, we applied
101 atmospheric pore pressure on the top surface,
34 pore pressure on the bottom surfaced,
and Zero flux for all side surfaces
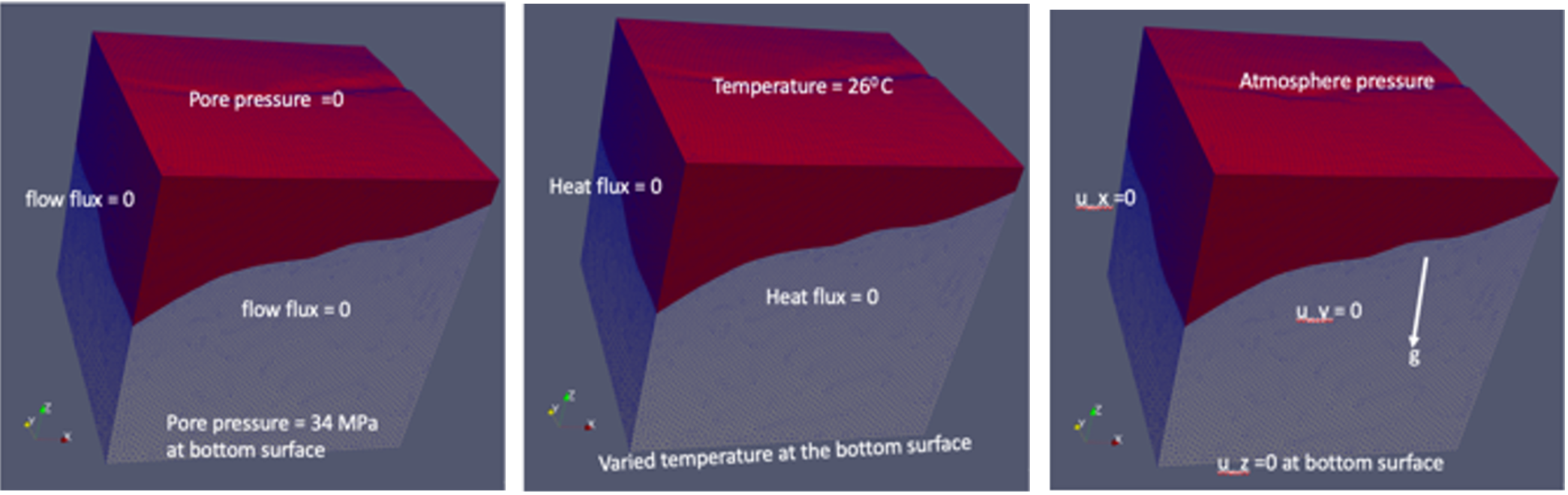
Figure 2: Illustration of boundary conditions for coupled three field.
The input lines are
[./pore_pressure_top]
type = DirichletBC
variable = pressure
boundary = 'surface_40m'
value = 101325 #atmospheric pressure in Pa-assumes water level at ground surface
[../]
[./pore_pressure_bottom]
type = DirichletBC
variable = pressure
boundary = 'bottom_40m'
value = 34000000
[../]
For heat transfer, we applied
26 atmospheric temperature on the top surface,
a distributed temperature on the bottom surface using a function
and zero heat flux boundary conditions for all side surfaces.
[./Side_Z_Minus_T]
type = FunctionDirichletBC
variable = temperature
boundary = 'bottom_40m'
function = T_on_face_Z_Minus
[../]
[./Side_Z_Plus_T]
type = DirichletBC
variable = temperature
boundary = 'surface_40m'
value= 299
[../]
[Functions] # temperature on boundary surfaces
[./T_on_face_Z_Minus]
type = PiecewiseBilinear0
data_file = bottom_2021_11_10_plus_50.csv
xaxis = 1
yaxis = 0
[../]
[]
Note the temperature unit is kelvin, and the temperature distribution function is built on the 'PiecewiseBilinear0' kernal using the x and y coordinates. The bottom_2021_11_10_plus_50.csv file contains the distributed temperature.
For the solid deformation, we applied
fixed displacement of the bottom and two side surfaces for the components perpendicular to each surface,
a uniform 101 atmospheric pressure at the top surface,
and normal tractions to the two side surface using the
zcoordinate independent functions.
[./roller_sigma_h_min]
type = DirichletBC
preset = true
variable = disp_i
value = 0
boundary = 'bottom_40m_granitoid_40m_front granitoid_40m_surface_40m_front'
[../]
[./roller_sigma_h_max]
type = DirichletBC
preset = true
variable = disp_j
value = 0
boundary = 'bottom_40m_granitoid_40m_right granitoid_40m_surface_40m_right'
[../]
[./bottom_z]
type = DirichletBC
preset = true
variable = disp_k
value = 0
boundary = 'bottom_40m'
[../]
[./S_h_min_normal]
type = FunctionNeumannBC
variable = disp_i
boundary = 'bottom_40m_granitoid_40m_back granitoid_40m_surface_40m_back'
function = '-15709*(1785-z)'
[../]
[./Side_Y_Plus_normal]
type = FunctionNeumannBC
variable = disp_j
boundary = 'bottom_40m_granitoid_40m_left granitoid_40m_surface_40m_left'
function = '-19640*(1785-z)'
[../]
[./Side_Z_Plus_traction_Z]
type = NeumannBC
variable = disp_k
boundary = 'surface_40m'
value = -101325
[../]
The negative sign of the atmospheric pressure indicates the opposite direction of pressure from traction.
Initial condition
We only initialized the pore pressure and temperature approximately using the same z depenedent functions as
[ICs]
[temperature]
type = FunctionIC
variable = temperature
function = '616 - ((2360+z)*7.615e-2)'
[]
[pressure]
type = FunctionIC
variable = pressure
function = '3.5317e7 - ((2360+z)*8455)'
[]
[]
Material parameters and constitutive models
Table 1 lists the values of the material parameters, in which we assume isotropic and homogeneous material distribution for each of the two layers. Accordingly, all the material values are constants, except a relative permeability was used for better convergence. The standard Equation of State for water & steam in IAPWS-IF97 is chosen for the fluid, and we assume the simulation domain is fully saturated with a single fluid phase. For mechanical deformation, a constant thermal expansion coefficient was used for both layers with a reference temperature of 20C, and the small strain linear elastic constitutive law was used.
Table 1: Material parameter values for the FORGE native state simulation
| Parameter | Unit | Sedimentary Layer Value | Granitoid Layer Value |
|---|---|---|---|
| Permeability | 1E-14 | 1E-18 | |
| Porosity | - | 0.12 | 0.001| |
| Grain density | kg/ | 2500 | 2750 |
| Specific heat | 830 | 790 | |
| Thermal conductivity | 2.8 | 3.05 | |
| Young's Modulus | GPa | 30 | 65 |
| Poisson's ratio | - | 0.3 | 0.3 |
| Biot Coefficient | - | 0.47 | 0.47 |
| Thermal expansion Coefficient | - | 6E-6| 6E-6 |
The complete material input section is
[Materials<<<{"href": "../syntax/Materials/index.html"}>>>]
#fluid properties and flow
[./permeability_sediment]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1e-14 0 0 0 1e-14 0 0 0 1e-14'
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
[../]
[./permeability_granite]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1e-18 0 0 0 1e-18 0 0 0 1e-18'
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
[../]
[./fluid_props]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = tabulated_water
phase<<<{"description": "The phase number"}>>> = 0
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
[../]
[./fluid_props_qp]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../source/materials/PorousFlowSingleComponentFluid.html"}>>>
phase<<<{"description": "The phase number"}>>> = 0
fp<<<{"description": "The name of the user object for fluid properties"}>>> = tabulated_water
[../]
[./porosity_sediment]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.12
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
[../]
[./porosity_granite]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.001
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
[../]
#rkp addition
[./ppss]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../source/materials/PorousFlow1PhaseP.html"}>>>
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[../]
[./ppss_qp]
type = PorousFlow1PhaseP<<<{"description": "This Material is used for the partially saturated single-phase situation where porepressure is the primary variable", "href": "../source/materials/PorousFlow1PhaseP.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = pressure
capillary_pressure<<<{"description": "Name of the UserObject defining the capillary pressure"}>>> = pc
[../]
[./massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../source/materials/PorousFlowMassFraction.html"}>>>
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
[../]
[./eff_fluid_pressure]
type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure. The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
[../]
[./eff_fluid_pressure_qp]
type = PorousFlowEffectiveFluidPressure<<<{"description": "This Material calculates an effective fluid pressure: effective_stress = total_stress + biot_coeff*effective_fluid_pressure. The effective_fluid_pressure = sum_{phases}(S_phase * P_phase)", "href": "../source/materials/PorousFlowEffectiveFluidPressure.html"}>>>
[../]
[./relperm]
type = PorousFlowRelativePermeabilityCorey<<<{"description": "This Material calculates relative permeability of the fluid phase, using the simple Corey model ((S-S_res)/(1-sum(S_res)))^n", "href": "../source/materials/PorousFlowRelativePermeabilityCorey.html"}>>>
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
n<<<{"description": "The Corey exponent of the phase."}>>> = 1
phase<<<{"description": "The phase number"}>>> = 0
[../]
#end rkp addition
#energy transport
[./temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../source/materials/PorousFlowTemperature.html"}>>>
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = temperature
[../]
[./temperature_nodal]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../source/materials/PorousFlowTemperature.html"}>>>
at_nodes<<<{"description": "Evaluate Material properties at nodes instead of quadpoints"}>>> = true
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = temperature
[../]
[./rock_heat_sediments]
type = PorousFlowMatrixInternalEnergy<<<{"description": "This Material calculates the internal energy of solid rock grains, which is specific_heat_capacity * density * temperature. Kernels multiply this by (1 - porosity) to find the energy density of the porous rock in a rock-fluid system", "href": "../source/materials/PorousFlowMatrixInternalEnergy.html"}>>>
specific_heat_capacity<<<{"description": "Specific heat capacity of the rock grains (J/kg/K)."}>>> = 830.0
density<<<{"description": "Density of the rock grains"}>>> = 2500
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
#density from Rick allis analysis, specific heat per tabulated values
[../]
[./rock_heat_granitoid]
type = PorousFlowMatrixInternalEnergy<<<{"description": "This Material calculates the internal energy of solid rock grains, which is specific_heat_capacity * density * temperature. Kernels multiply this by (1 - porosity) to find the energy density of the porous rock in a rock-fluid system", "href": "../source/materials/PorousFlowMatrixInternalEnergy.html"}>>>
specific_heat_capacity<<<{"description": "Specific heat capacity of the rock grains (J/kg/K)."}>>> = 790.0
density<<<{"description": "Density of the rock grains"}>>> = 2750
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
#density from Rick allis analysis, specific heat per tabulated values
[../]
[./thermal_conductivity_sediments]
type = PorousFlowThermalConductivityIdeal<<<{"description": "This Material calculates rock-fluid combined thermal conductivity by using a weighted sum. Thermal conductivity = dry_thermal_conductivity + S^exponent * (wet_thermal_conductivity - dry_thermal_conductivity), where S is the aqueous saturation", "href": "../source/materials/PorousFlowThermalConductivityIdeal.html"}>>>
dry_thermal_conductivity<<<{"description": "The thermal conductivity of the rock matrix when the aqueous saturation is zero"}>>> = '2.8 0 0 0 2.8 0 0 0 2.8'
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
[../]
[./thermal_conductivity_granitoid]
type = PorousFlowThermalConductivityIdeal<<<{"description": "This Material calculates rock-fluid combined thermal conductivity by using a weighted sum. Thermal conductivity = dry_thermal_conductivity + S^exponent * (wet_thermal_conductivity - dry_thermal_conductivity), where S is the aqueous saturation", "href": "../source/materials/PorousFlowThermalConductivityIdeal.html"}>>>
dry_thermal_conductivity<<<{"description": "The thermal conductivity of the rock matrix when the aqueous saturation is zero"}>>> = '3.05 0 0 0 3.05 0 0 0 3.05'
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
[../]
#mechanics
[./density_sediment]
type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
prop_names<<<{"description": "The names of the properties this material will have"}>>> = density
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
prop_values<<<{"description": "The values associated with the named properties"}>>> = 2500.0
[../]
[./density_granitoid]
type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
prop_names<<<{"description": "The names of the properties this material will have"}>>> = density
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
prop_values<<<{"description": "The values associated with the named properties"}>>> = 2750.0
[../]
[./biot]
type = GenericConstantMaterial<<<{"description": "Declares material properties based on names and values prescribed by input parameters.", "href": "../source/materials/GenericConstantMaterial.html"}>>>
prop_names<<<{"description": "The names of the properties this material will have"}>>> = biot_coefficient
prop_values<<<{"description": "The values associated with the named properties"}>>> = 0.47
[../]
[./elasticity_sediment]
type = ComputeIsotropicElasticityTensor<<<{"description": "Compute a constant isotropic elasticity tensor.", "href": "../source/materials/ComputeIsotropicElasticityTensor.html"}>>>
youngs_modulus<<<{"description": "Young's modulus of the material."}>>> = 3.0e+10
poissons_ratio<<<{"description": "Poisson's ratio for the material."}>>> = 0.3
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = granitoid_40m_surface_40m
[../]
[./elasticity_granitoid]
type = ComputeIsotropicElasticityTensor<<<{"description": "Compute a constant isotropic elasticity tensor.", "href": "../source/materials/ComputeIsotropicElasticityTensor.html"}>>>
youngs_modulus<<<{"description": "Young's modulus of the material."}>>> = 6.2e+10
poissons_ratio<<<{"description": "Poisson's ratio for the material."}>>> = 0.3
block<<<{"description": "The list of blocks (ids or names) that this object will be applied"}>>> = bottom_40m_granitoid_40m
[../]
[./thermal_expansion_strain]
type = ComputeThermalExpansionEigenstrain<<<{"description": "Computes eigenstrain due to thermal expansion with a constant coefficient", "href": "../source/materials/ComputeThermalExpansionEigenstrain.html"}>>>
stress_free_temperature<<<{"description": "Reference temperature at which there is no thermal expansion for thermal eigenstrain calculation"}>>> = 293
thermal_expansion_coeff<<<{"description": "Thermal expansion coefficient"}>>> = 2.0E-6
temperature<<<{"description": "Coupled temperature"}>>> = temperature
eigenstrain_name<<<{"description": "Material property name for the eigenstrain tensor computed by this model. IMPORTANT: The name of this property must also be provided to the strain calculator."}>>> = eigenstrain
[../]
[./strain]
type = ComputeSmallStrain<<<{"description": "Compute a small strain.", "href": "../source/materials/ComputeSmallStrain.html"}>>>
[../]
[./stress]
type = ComputeLinearElasticStress<<<{"description": "Compute stress using elasticity for small strains", "href": "../source/materials/ComputeLinearElasticStress.html"}>>>
[../]
[]Postprocessor and Excution
In order to validate the simulation, we extract the temperature, pore pressure and stress tensor distribution along the survey wells in FORGE, which include wells 16A, 58-32, 78-32, 78B-32, and 56-32. This was achived via the PointValueSampler sampler via the well trajectory coordinates.
A steady state solver was requested in the Executioner section as
[Executioner<<<{"href": "../syntax/Executioner/index.html"}>>>]
type = Steady
solve_type = Newton
l_tol = 1e-3
l_max_its = 2000
nl_max_its = 200
nl_abs_tol = 1e-4
nl_rel_tol = 1e-4
[]Results
Figure 3 presents the simulated results along the trajectory of Well 56-32, a comparison between the in situ measurement and the prediction indicate the accuracy of the simulation.
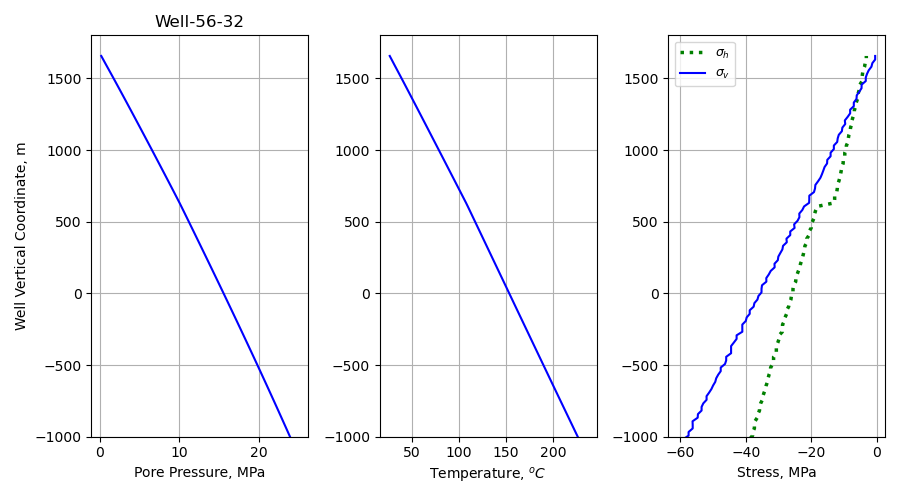
Figure 3: Pore pressure, temperature, and stress distribution along the trajectory of the Well 56-32.
References
- Ruijie Liu, Rob Podgorney, Aleta Finnila, Pengju Xing, John McLennan, and Joe Moore.
Development of a coupled multi-field utah forge native state model: phase 3 update.
In GRC Transactions, volume 46. 2022.[BibTeX]