Flow and Solute Transport in Porous Media
1D solute transportation
Problem statement
This example is based on Karmakar et al. (2022). The transportation of tracer in water in a 1D porous tank is modelled. The schematic is demonstrated in Figure 1. The experiment details are elaborated in the referred paper so will not be shown here to avoid repetition. The governing equations are provided below:
(1)
(2)
Notation used in these equations is summarised in the nomenclature.
Table 1: Parameters of the problem .
| Symbol | Quantity | Value | Units |
|---|---|---|---|
| Porosity | |||
| Permeability | |||
| Viscosity () | |||
| Gravity | |||
| Initial temperature | |||
| Total time | days |
.](../../media/porous_flow/schematic_tracer.png)
Figure 1: The schematic of the problem Karmakar et al. (2022).
Input file setup
This section describes the input file syntax.
Mesh
The first step is to set up the mesh. In this problem, a tank with a length of 100 m is simulated and an element size of 1 m is used.
[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
[gen]
type = GeneratedMeshGenerator<<<{"description": "Create a line, square, or cube mesh with uniformly spaced or biased elements.", "href": "../../source/meshgenerators/GeneratedMeshGenerator.html"}>>>
dim<<<{"description": "The dimension of the mesh to be generated"}>>> = 1
nx<<<{"description": "Number of elements in the X direction"}>>> = 100
xmin<<<{"description": "Lower X Coordinate of the generated mesh"}>>> = 0
xmax<<<{"description": "Upper X Coordinate of the generated mesh"}>>> = 100
[]
[]Fluid properties
After the mesh has been specified, we need to provide the fluid properties that are used for this simulation. For our case, it will be just water and can be easily implemented as follows:
[FluidProperties<<<{"href": "../../syntax/FluidProperties/index.html"}>>>]
[water]
type = Water97FluidProperties<<<{"description": "Fluid properties for water and steam (H2O) using IAPWS-IF97", "href": "../../source/fluidproperties/Water97FluidProperties.html"}>>>
[]
[]Variables declaration
Then, we need to declare what type of unknown we are solving. This can be done in the variable code block. Since we are focusing on the concentration of tracer at x =50 m, C is a desired variable. Porepressure is also used for the fluid motion. Since we only have constant initial conditions so they can be directly supplied here.
[Variables<<<{"href": "../../syntax/Variables/index.html"}>>>]
[porepressure]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 1e5
[]
[C]
initial_condition<<<{"description": "Specifies a constant initial condition for this variable"}>>> = 0
[]
[]Kernel declaration
This section describes the physics we need to solve. To do so, some kernels are declared. In MOOSE, the required kernels depend on the terms in the governing equations. For this problem, six kernels were declared. To have a better understanding, users are recommended to visit this page. The code block is shown below with the first three kernels associated with equation 1 and the remain associated with equation 2.
[Kernels<<<{"href": "../../syntax/Kernels/index.html"}>>>]
[mass_der_water]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
[]
[adv_pp]
type = PorousFlowFullySaturatedDarcyFlow<<<{"description": "Darcy flux suitable for models involving a fully-saturated single phase, multi-component fluid. No upwinding is used", "href": "../../source/kernels/PorousFlowFullySaturatedDarcyFlow.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
[]
[diff_pp]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = ${disp}
[]
[mass_der_C]
type = PorousFlowMassTimeDerivative<<<{"description": "Derivative of fluid-component mass with respect to time. Mass lumping to the nodes is used.", "href": "../../source/kernels/PorousFlowMassTimeDerivative.html"}>>>
fluid_component<<<{"description": "The index corresponding to the component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
[]
[adv_C]
type = PorousFlowFullySaturatedDarcyFlow<<<{"description": "Darcy flux suitable for models involving a fully-saturated single phase, multi-component fluid. No upwinding is used", "href": "../../source/kernels/PorousFlowFullySaturatedDarcyFlow.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
[]
[diff_C]
type = PorousFlowDispersiveFlux<<<{"description": "Dispersive and diffusive flux of the component given by fluid_component in all phases", "href": "../../source/kernels/PorousFlowDispersiveFlux.html"}>>>
fluid_component<<<{"description": "The index corresponding to the fluid component for this kernel"}>>> = 0
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
disp_trans<<<{"description": "Vector of transverse dispersion coefficients for each phase"}>>> = 0
disp_long<<<{"description": "Vector of longitudinal dispersion coefficients for each phase"}>>> = ${disp}
[]
[]Material setup
Additional material properties are required , which are declared here:
[Materials<<<{"href": "../../syntax/Materials/index.html"}>>>]
[ps]
type = PorousFlow1PhaseFullySaturated<<<{"description": "This Material is used for the fully saturated single-phase situation where porepressure is the primary variable", "href": "../../source/materials/PorousFlow1PhaseFullySaturated.html"}>>>
porepressure<<<{"description": "Variable that represents the porepressure of the single phase"}>>> = porepressure
[]
[porosity]
type = PorousFlowPorosityConst<<<{"description": "This Material calculates the porosity assuming it is constant", "href": "../../source/materials/PorousFlowPorosityConst.html"}>>>
porosity<<<{"description": "The porosity (assumed indepenent of porepressure, temperature, strain, etc, for this material). This should be a real number, or a constant monomial variable (not a linear lagrange or other kind of variable)."}>>> = 0.25
[]
[permeability]
type = PorousFlowPermeabilityConst<<<{"description": "This Material calculates the permeability tensor assuming it is constant", "href": "../../source/materials/PorousFlowPermeabilityConst.html"}>>>
permeability<<<{"description": "The permeability tensor (usually in m^2), which is assumed constant for this material"}>>> = '1E-11 0 0 0 1E-11 0 0 0 1E-11'
[]
[water]
type = PorousFlowSingleComponentFluid<<<{"description": "This Material calculates fluid properties at the quadpoints or nodes for a single component fluid", "href": "../../source/materials/PorousFlowSingleComponentFluid.html"}>>>
fp<<<{"description": "The name of the user object for fluid properties"}>>> = water
phase<<<{"description": "The phase number"}>>> = 0
[]
[massfrac]
type = PorousFlowMassFraction<<<{"description": "This Material forms a std::vector<std::vector ...> of mass-fractions out of the individual mass fractions", "href": "../../source/materials/PorousFlowMassFraction.html"}>>>
mass_fraction_vars<<<{"description": "List of variables that represent the mass fractions. Format is 'f_ph0^c0 f_ph0^c1 f_ph0^c2 ... f_ph0^c(N-2) f_ph1^c0 f_ph1^c1 fph1^c2 ... fph1^c(N-2) ... fphP^c0 f_phP^c1 fphP^c2 ... fphP^c(N-2)' where N=num_components and P=num_phases, and it is assumed that f_ph^c(N-1)=1-sum(f_ph^c,{c,0,N-2}) so that f_ph^c(N-1) need not be given. If no variables are provided then num_phases=1=num_components."}>>> = C
[]
[temperature]
type = PorousFlowTemperature<<<{"description": "Material to provide temperature at the quadpoints or nodes and derivatives of it with respect to the PorousFlow variables", "href": "../../source/materials/PorousFlowTemperature.html"}>>>
temperature<<<{"description": "Fluid temperature variable. Note, the default is suitable if your simulation is using Kelvin units, but probably not for Celsius"}>>> = 293
[]
[diff]
type = PorousFlowDiffusivityConst<<<{"description": "This Material provides constant tortuosity and diffusion coefficients", "href": "../../source/materials/PorousFlowDiffusivityConst.html"}>>>
diffusion_coeff<<<{"description": "List of diffusion coefficients. Order is i) component 0 in phase 0; ii) component 1 in phase 0 ...; component 0 in phase 1; ... component k in phase n (m^2/s"}>>> = '0 0'
tortuosity<<<{"description": "List of tortuosities. Order is i) phase 0; ii) phase 1; etc"}>>> = 0.1
[]
[relperm]
type = PorousFlowRelativePermeabilityConst<<<{"description": "This class sets the relative permeability to a constant value (default = 1)", "href": "../../source/materials/PorousFlowRelativePermeabilityConst.html"}>>>
kr<<<{"description": "Relative permeability"}>>> = 1
phase<<<{"description": "The phase number"}>>> = 0
[]
[]Boundary Conditions
The next step is to supply the boundary conditions. There are three Dirichlet boundary conditions that we need to supply. The first two are constant pressure at the inlet and outlet denoted as constant_inlet_pressure and constant_outlet_porepressure. Another one is constant tracer concentration at the inlet denoted as inlet_tracer. Finally, a PorousFlowOutflowBC boundary condition was supplied at the outlet to allow the tracer to freely move out of the domain.
[BCs<<<{"href": "../../syntax/BCs/index.html"}>>>]
[constant_inlet_pressure]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
value<<<{"description": "Value of the BC"}>>> = 1.2e5
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
[]
[constant_outlet_porepressure]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
value<<<{"description": "Value of the BC"}>>> = 1e5
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
[]
[inlet_tracer]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
value<<<{"description": "Value of the BC"}>>> = 0.001
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
[]
[outlet_tracer]
type = PorousFlowOutflowBC<<<{"description": "Applies an 'outflow' boundary condition, which allows fluid components or heat energy to flow freely out of the boundary as if it weren't there. This is fully upwinded", "href": "../../source/bcs/PorousFlowOutflowBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
mass_fraction_component<<<{"description": "The index corresponding to a fluid component. If supplied, the residual contribution will be multiplied by the mass fraction, corresponding to allowing the given mass fraction to flow freely from the boundary. This is ignored if flux_type = heat"}>>> = 0
[]
[]Executioner setup
For this problem, a transient solver is required. To save time and computational resources, IterationAdaptiveDT was implemented. This option enables the time step to be increased if the solution converges and decreased if it does not. Thus, this will help save time if a large time step can be used and aid in convergence if a small time step is required. For practice, users can try to disable it by putting the code block into comment and witnessing the difference in the solving time and solution.
[Executioner<<<{"href": "../../syntax/Executioner/index.html"}>>>]
type = Transient
end_time = 17280000
dtmax = 86400
nl_rel_tol = 1e-6
nl_abs_tol = 1e-12
[TimeStepper<<<{"href": "../../syntax/Executioner/TimeStepper/index.html"}>>>]
type = IterationAdaptiveDT
dt = 1000
[]
[]Auxiliary kernels and variables (optional)
This section is optional since these kernels and variables do not affect the calculation of the desired variable. In this example, we want to know the Darcy velocity in the x direction thus we will add an auxkernel and an auxvariable for it.
[AuxVariables<<<{"href": "../../syntax/AuxVariables/index.html"}>>>]
[Darcy_vel_x]
order<<<{"description": "Specifies the order of the FE shape function to use for this variable (additional orders not listed are allowed)"}>>> = CONSTANT
family<<<{"description": "Specifies the family of FE shape functions to use for this variable"}>>> = MONOMIAL
[]
[][AuxKernels<<<{"href": "../../syntax/AuxKernels/index.html"}>>>]
[Darcy_vel_x]
type = PorousFlowDarcyVelocityComponent<<<{"description": "Darcy velocity (in m^3.s^-1.m^-2, or m.s^-1) -(k_ij * krel /mu (nabla_j P - w_j)), where k_ij is the permeability tensor, krel is the relative permeability, mu is the fluid viscosity, P is the fluid pressure, and w_j is the fluid weight.", "href": "../../source/auxkernels/PorousFlowDarcyVelocityComponent.html"}>>>
variable<<<{"description": "The name of the variable that this object applies to"}>>> = Darcy_vel_x
component<<<{"description": "The spatial component of the Darcy flux to return"}>>> = x
fluid_phase<<<{"description": "The index corresponding to the fluid phase"}>>> = 0
[]
[]Postprocessor
As previously discussed, we only want to know the variation of concentration (C) and x-direction Darcy velocity at x=50 m over time. So, we need to tell MOOSE to only write that information into the result file via this code block.
[Postprocessors<<<{"href": "../../syntax/Postprocessors/index.html"}>>>]
[C]
type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../source/postprocessors/PointValue.html"}>>>
variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = C
point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '50 0 0'
[]
[Darcy_x]
type = PointValue<<<{"description": "Compute the value of a variable at a specified location", "href": "../../source/postprocessors/PointValue.html"}>>>
variable<<<{"description": "The name of the variable that this postprocessor operates on."}>>> = Darcy_vel_x
point<<<{"description": "The physical point where the solution will be evaluated."}>>> = '50 0 0'
[]
[]Result
The results obtained from MOOSE are compared against the analytical solution proposed by Ogata et al. (1961).
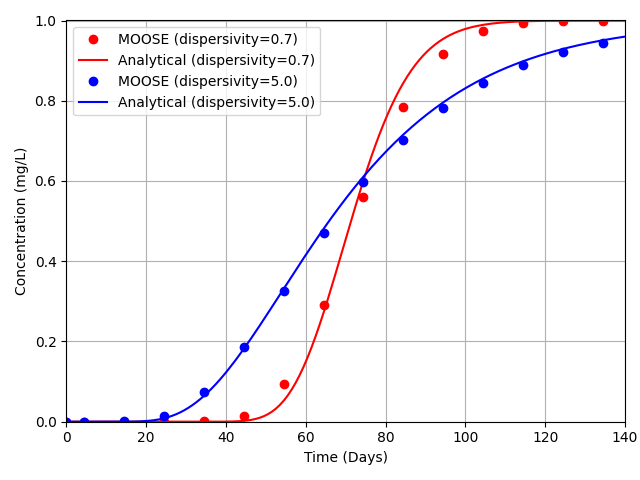
Figure 2: Tracer concentration with respect to time.
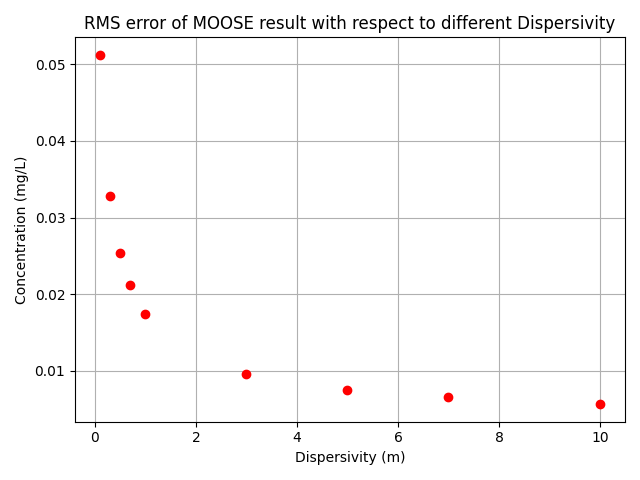
Figure 3: Root-mean-square error of MOOSE results.
Compared with the benchmark conducted by Karmakar et al. (2022), it can be seen that MOOSE is capable of delivering accurate results for this type of problem.
.](../../media/porous_flow/benchmark_tracer.png)
Figure 4: The benchmark conducted by Karmakar et al. (2022).
2D solute transportation
Problem statement
This example is based on Karmakar et al. (2022). The transportation of tracer in water in a 2D porous tank is modelled. The schematic is demonstrated in Figure 5. The parameters are the same as the 1D problem as provided in Table 1.
.](../../media/porous_flow/schematic_tracer_2D.png)
Figure 5: The schematic of the 2D problem Karmakar et al. (2022).
Input file setup
The input file for this problem is similar to the 1D case except for some changes made to account for the 2D mesh and the changes in the boundary conditions which are elaborated in the following sections. Other sections will be the same as the 1D case.
Mesh
For this problem, to simulate a 2D rectangular aquifer with a point source placed at the origin, the x-domain was chosen from -50 to 50 m and the y-domain from 0 to 50 m.
[Mesh<<<{"href": "../../syntax/Mesh/index.html"}>>>]
[gen]
type = GeneratedMeshGenerator<<<{"description": "Create a line, square, or cube mesh with uniformly spaced or biased elements.", "href": "../../source/meshgenerators/GeneratedMeshGenerator.html"}>>>
dim<<<{"description": "The dimension of the mesh to be generated"}>>> = 2
nx<<<{"description": "Number of elements in the X direction"}>>> = 100
xmin<<<{"description": "Lower X Coordinate of the generated mesh"}>>> = -50
xmax<<<{"description": "Upper X Coordinate of the generated mesh"}>>> = 50
ny<<<{"description": "Number of elements in the Y direction"}>>> = 60
ymin<<<{"description": "Lower Y Coordinate of the generated mesh"}>>> = 0
ymax<<<{"description": "Upper Y Coordinate of the generated mesh"}>>> = 50
[]
[]DiracKernels set-up
Since our problem comprises a point source, PorousFlowSquarePulsePointSource DiracKernels are required. These DiracKernels inject the water and tracer into the domain at a constant rate. As can be seen below, two DiracKernels are used. The first one supplies the water with a specified mass flux to the system and the second one the tracer.
[DiracKernels<<<{"href": "../../syntax/DiracKernels/index.html"}>>>]
[source_P]
type = PorousFlowSquarePulsePointSource<<<{"description": "Point source (or sink) that adds (removes) fluid at a constant mass flux rate for times between the specified start and end times.", "href": "../../source/dirackernels/PorousFlowSquarePulsePointSource.html"}>>>
point<<<{"description": "The x,y,z coordinates of the point source (sink)"}>>> = '0 0 0'
mass_flux<<<{"description": "The mass flux at this point in kg/s (positive is flux in, negative is flux out)"}>>> = 1e-1
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
[]
[source_C]
type = PorousFlowSquarePulsePointSource<<<{"description": "Point source (or sink) that adds (removes) fluid at a constant mass flux rate for times between the specified start and end times.", "href": "../../source/dirackernels/PorousFlowSquarePulsePointSource.html"}>>>
point<<<{"description": "The x,y,z coordinates of the point source (sink)"}>>> = '0 0 0'
mass_flux<<<{"description": "The mass flux at this point in kg/s (positive is flux in, negative is flux out)"}>>> = 1e-7
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
[]
[]Boundary Conditions
The boundary conditions are similar to the 1D case except for the addition of several Dirichlet, and outflow conditions due to the extra faces of the 2D problem. The bottom face was not supplied with any boundary condition as it a line of symmetry (only half the model is simulated). Therefore, no-flow is allowed across this boundary.
[BCs<<<{"href": "../../syntax/BCs/index.html"}>>>]
[constant_outlet_porepressure_]
type = DirichletBC<<<{"description": "Imposes the essential boundary condition $u=g$, where $g$ is a constant, controllable value.", "href": "../../source/bcs/DirichletBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = porepressure
value<<<{"description": "Value of the BC"}>>> = 1e5
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = 'top left right'
[]
[outlet_tracer_top]
type = PorousFlowOutflowBC<<<{"description": "Applies an 'outflow' boundary condition, which allows fluid components or heat energy to flow freely out of the boundary as if it weren't there. This is fully upwinded", "href": "../../source/bcs/PorousFlowOutflowBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = top
mass_fraction_component<<<{"description": "The index corresponding to a fluid component. If supplied, the residual contribution will be multiplied by the mass fraction, corresponding to allowing the given mass fraction to flow freely from the boundary. This is ignored if flux_type = heat"}>>> = 0
[]
[outlet_tracer_right]
type = PorousFlowOutflowBC<<<{"description": "Applies an 'outflow' boundary condition, which allows fluid components or heat energy to flow freely out of the boundary as if it weren't there. This is fully upwinded", "href": "../../source/bcs/PorousFlowOutflowBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = right
mass_fraction_component<<<{"description": "The index corresponding to a fluid component. If supplied, the residual contribution will be multiplied by the mass fraction, corresponding to allowing the given mass fraction to flow freely from the boundary. This is ignored if flux_type = heat"}>>> = 0
[]
[outlet_tracer_left]
type = PorousFlowOutflowBC<<<{"description": "Applies an 'outflow' boundary condition, which allows fluid components or heat energy to flow freely out of the boundary as if it weren't there. This is fully upwinded", "href": "../../source/bcs/PorousFlowOutflowBC.html"}>>>
variable<<<{"description": "The name of the variable that this residual object operates on"}>>> = C
boundary<<<{"description": "The list of boundary IDs from the mesh where this object applies"}>>> = left
mass_fraction_component<<<{"description": "The index corresponding to a fluid component. If supplied, the residual contribution will be multiplied by the mass fraction, corresponding to allowing the given mass fraction to flow freely from the boundary. This is ignored if flux_type = heat"}>>> = 0
[]
[]Result
The results obtained from MOOSE are compared against the analytical solution proposed by Schroth et al. (2000).
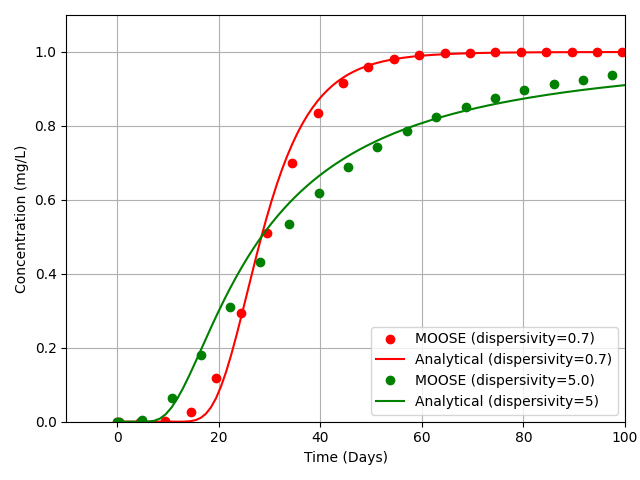
Figure 6: Tracer concentration with respect to time.
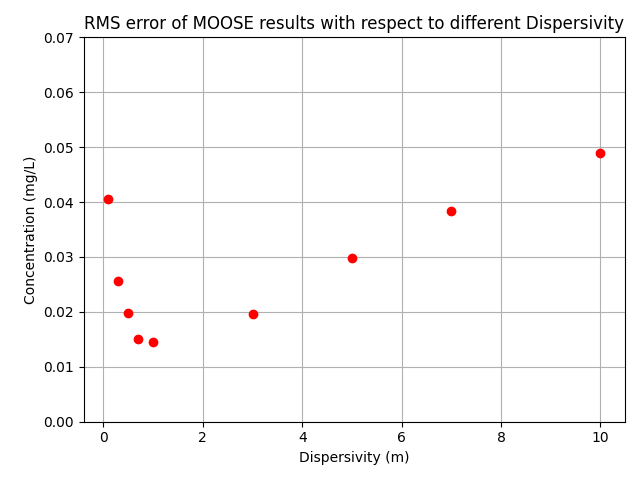
Figure 7: Root-mean-square error of MOOSE results.
Compared with the benchmark conducted by Karmakar et al. (2022), it can be seen that once again MOOSE is capable of delivering accurate results for this type of problem.
.](../../media/porous_flow/benchmark_tracer_2D.png)
Figure 8: The benchmark conducted by Karmakar et al. (2022).
References
- Shyamal Karmakar, Alexandru Tatomir, Sandra Oehlmann, Markus Giese, and Martin Sauter.
Numerical benchmark studies on flow and solute transport in geological reservoirs.
Water, 2022.
URL: https://www.mdpi.com/2073-4441/14/8/1310, doi:10.3390/w14081310.[BibTeX]
- Akio Ogata, Robert B. Banks, Stewart Lee Udall, and Thomas B Nolan.
A solution of the differential equation of longitudinal dispersion in porous media.
Technical Report, United States Department of the Interior, 1961.
URL: https://api.semanticscholar.org/CorpusID:117806845.[BibTeX]
- M.H Schroth, Jonathan Istok, and Roy Haggerty.
In situ evaluation of solute retardation using single-well push–pull tests.
Advances in Water Resources, 24:105–117, 10 2000.
doi:10.1016/S0309-1708(00)00023-3.[BibTeX]